SaiBook.us Geometry

Lesson Example Discussion Quiz: Class Homework

Example

Title: Volume of 3d-shapes(sphere, prism)

Grade: 4-a Lesson: S3-L3

Explanation: The best way to understand geometry is by looking at some examples. Take turns and read each example for easy understanding.

Examples:

The rectangular prism has a length of 12 feet, a width of 8 feet, and a surface area of 432 square feet. Find its volume.

Step 1a

Given a rectangular prism with a surface area of 432 square feet, a length of 12 feet, and a width of 8 feet, we need to find its volume.

The formula for the surface area (A) of a rectangular prism is given by: A = 2lw + 2lh + 2wh

Here, l, w, and h represent the length, width, and height of the prism, respectively.

$1a$

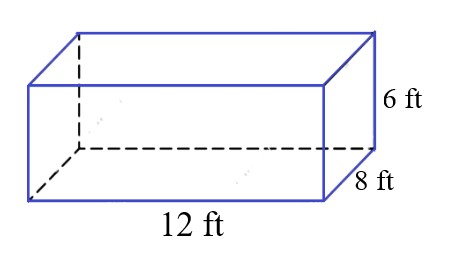
Explanation: Given a surface area of 432 sq. ft, a length of 12 ft, and a width of 8 ft, determine the volume of the rectangular prism using the formula : A = 2lw + 2lh + 2wh.

Step 1b

Formulating an equation with the provided details: 432 = 2(12)(8) + 2(12)h + 2(8)h

Simplifying yields : 432 = 192 + 24h + 16h

which further combines to 432 = 192 + 50h

Subtract 192 on both sides: 432 - 192 = 192 -192 + 50h

240 = 40h

Solving for h, h = \$240/60\$ = 6.

Explanation: In this stage, determine the height. Set up the equation using the provided details:

432 = 2(12)(8) + 2(12)h + 2(8)h. Simplify to 240 = 40h and solve for h, h = \$240/60\$ = 6.

Step 1c

The formula for finding the volume of a rectangular prism : V = lwh

To find the volume when the height is 6 ft, use the formula: V = 12(8)(6) = 576 cubic feet.

So, the volume of the rectangular prism is 576 cubic feet.

Explanation: To determine the volume of a rectangular prism with a height of 6 ft, use the formula V = lwh, resulting in V = 12(8)(6) = 576 cubic feet.