SaiBook.us Geometry

Lesson Example Discussion Quiz: Class Homework

Lesson

Title: Surface area of 3D shapes(Cube, cuboid, Cone)

Grade: 4-a Lesson: S3-L1

Explanation: Hello students, let us learn a new topic in geometry today with definitions, concepts, examples, and worksheets included.

Lesson:

Definition: Cube

A cube is a three-dimensional solid with six square faces, eight vertices, and 12 edges. Three faces meet at each vertex, making it a specific instance of a regular hexahedron.

The surface area (A) can be determined with the formula \$"A" = 6s^2\$. Where 's' denotes the length of a side.

$1$

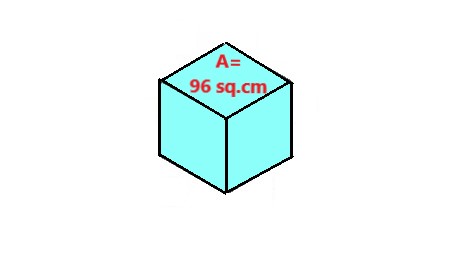
Explanation: In this image, if a cube has a surface area of 96 sq.cm and a side length of 4 cm, the surface area can be calculated using \$"A" = 6s²\$.

Definition: Cuboid

A cuboid, also known as a rectangular prism, is a three-dimensional solid shape characterized by six rectangular faces, eight vertices, and twelve edges, making it a convex polyhedron.

The surface area (A = 2lw + 2lh + 2wh), and diagonal length \$("d" = \sqrt(l^2 + w^2 + h^2))\$, where l, w, and h represent the length, width, and height, respectively.

$2$

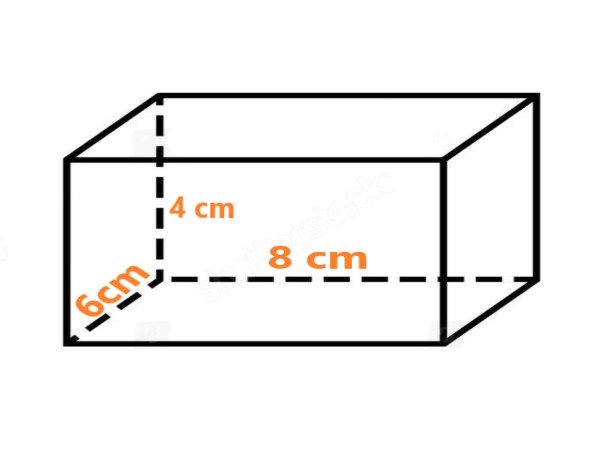
Explanation: The image displays a cuboid with a Lateral surface area(LSA) of 112 sq. cm, determined by the dimensions l = 8 cm, b = 6 cm, and h = 4 cm, utilizing the formula LSA = 2h(l + b).

Definition: Cone

A cone, a three-dimensional geometric form, consists of a circular base linked to a sole vertex.

The surface area A = \$(πr^2 + πr^2l)\$ and slant heigth l = \$(\sqrt(r^2 + h^2))\$.

$3$

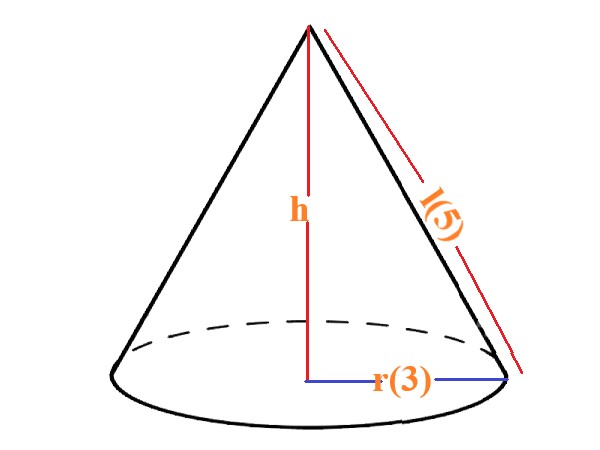
Explanation: In this image, the cone exhibits a total surface area measuring 75.36 sq.cm, determined with a radius of 3 cm and a slant height of 5 cm, using the formula A = πr(l + r).