Step 1a

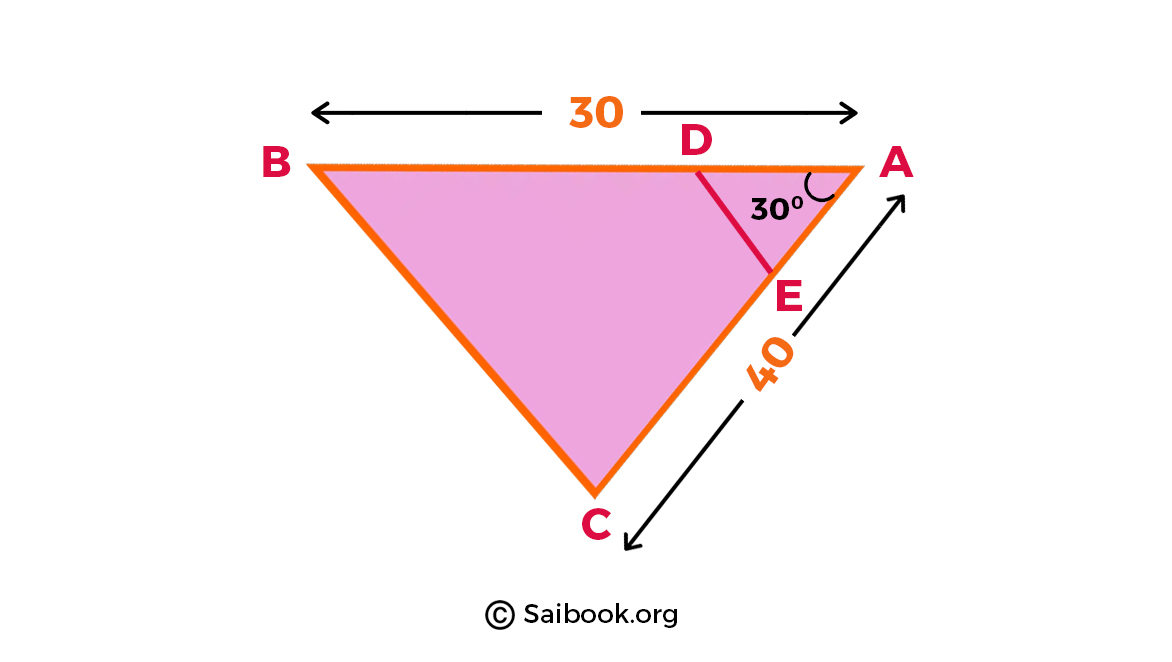
Explanation: AB is 30 units long, AC is 40 units long, and angle A is 30°.

Step 1b

Now, we can use the area of the triangle formula: sin30º = \$1/2\$

Area ΔABC = \$1/2 \times AB \times AC \times sin(A)\$

⇒ \$1/2 \times 30 \times 40 \times sin30º\$ = 300 square units.

Explanation: Using the formula for the area of a triangle, we get Area ΔABC = \$1/2 \times AB \times AC \times sin(A)\$, which gives us an area of 300 square units for triangle ABC with sides AB = 30 and AC = 40 and angle A = 30º.

Step 1c

Given D divides AB in the ratio of 1:2, AD = \$1 /(1 + 2)\$

AB = \$1/3 \times 30\$ = 10 sq.units.

Explanation: AB is divided by D in the ratio of 1:2, and AD is \$1/3\$ of AB.

Step 1d

Given that E is the midpoint of AC, thus AE = \$(AC)/2 = 40/2\$ = \$20 units^2\$.

Explanation: Given that E is the midpoint of AC, we have AE = \$20 units^2\$. since AE = \$(AC)/2\$ = \$40/2\$.

Step 1e

Now, we find the area of the triangle. Area ΔADE = \$1/2 \times AD \times AE \times sin(A)\$ = \$1/2 \times 10 \times 20 \times sin(30º)\$ = 50 square units.

Explanation: Now, let’s find the area of the triangle. The area of triangle ΔADE is equal to half of the product of AD, AE, and the sine of angle A.

So, Area ΔADE = \$1/2 \times AD \times AE \times sin(A)\$.

⇒ \$1/2 \times 10 \times 20 \times sin(30º)\$ = 50 square units.

Step 1f

Area(BCED) = Area ΔABC - Area ΔADE

⇒ 300 - 50 = 250 square units

Explanation: To find the area of a trapezoid with vertices B, C, E, and D, you can use the formula: Area(BCED) = Area of ΔABC - Area of ΔADE. When you plug in the numbers, you get 300 - 50 = 250 square units.

Step 1g

The area of the triangle (BCED) has been calculated to be 250 square units.

Explanation: The area of the triangle BCED is equal to 250 square units.