SaiBook.us Fractions

Lesson Example Discussion Quiz: Class Homework

Example

Title: Equivalent Fraction

Grade: 4-a Lesson: S2-L2

Explanation: Hello Students, time to learn examples. Let us take turns and read each example. Explain each step. Pay special attention to steps and pictures and communicate in your own words.

Examples:

Find the missing number in the given equivalent fraction: \$10/12 = ?/36 = 90/108\$

Step 1a

The fraction stem [10/12]can be simplified by dividing both the numerator and denominator by their greatest common divisor, which is 2. This gives the stem [5/6].

The fraction \$90/108\$can be simplified by dividing both the numerator and denominator by their greatest common divisor, which is 18. This gives \$5/6\$. Simplified the fraction \$5/6\$ = \$?/36\$ = \$5/6\$.

$1a$

Explanation: In this step, to simplify fractions, divide the numerator and denominator by their greatest common divisor (GCD). For this instance, \$10/12\$ and \$90/108\$ can be simplified by finding their GCD.

The GCD of 10 and 12 is 2, and the GCD of 90 and 108 is 18.

So, \$10/12\$ simplifies to \$5/6\$, \$90/108\$ simplifies to \$5/6\$.

Step 1b

The second fraction \$?/36\$ is equivalent to \$5/6\$, we can set up a proportion to find the missing number: \$ ?/36\$ = \$5/6\$

$1b$

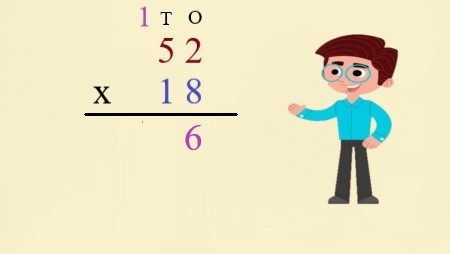
Explanation: The fraction stem [x/36] is equivalent to [5/6]. To find the missing number, we can set up a proportion: \$ x/36\$ = \$5/6\$

Step 1c

To solve for the missing numerator, we cross multiply: \$x \times 6\$ = \$5 \times 36\$ \$6x = 108\$ ⇒ \$x = 108/6\$ x = 30

So, the missing number in the given equivalent fraction is 30.

$1c$

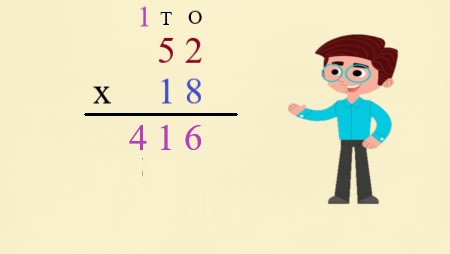
Explanation: In this step, find the missing numerator, cross-multiply both sides of the equation, and solve for x. 6x = 5 x 36, which simplifies to x = 30.

Therefore, the missing number in the given equivalent fraction is 30.