SaiBook.us Algebra

Lesson Example Discussion Quiz: Class Homework

Lesson

Title: Multiplying Radicals

Grade: 8-b Lesson: S1-L7

Explanation: Hello students, let us learn a new topic in algebra today with definitions, concepts, examples, and worksheets included.

Lesson:

Definition: Multiplying Radicals

To multiply radicals, multiply the coefficients (numbers outside the radical) and the radicands (numbers inside the radical) together, then simplify the resulting expression if possible.

Product of Radicals Rule: \$ \sqrt(a) \times \sqrt(b) = \sqrt(a \times b) \$
This means that you can multiply the numbers inside the radicals and then take the square root of the product.
Same Index Rule: \$ root(n)(a) \times root(n)(b) = root(n)(a \times b) \$
When multiplying radicals with the same index, you multiply the radicands (the numbers inside the radical signs) and keep the same index.
Different Index Rule: When the radicals have different indices, it’s usually more complex. Typically, you need to express them with a common index before multiplying.

$1$

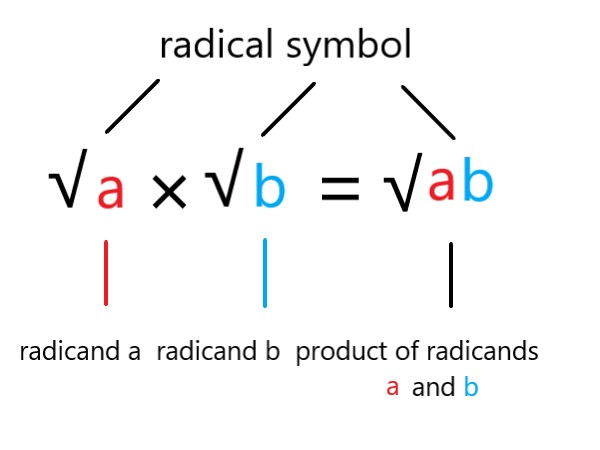
Explanation: The image shows how to multiply two radicals:

Radical Symbols (√): These symbols represent square roots.
Radicands: \$ \sqrt a \$: "a" is the number inside the first square root.\$ \sqrt b \$: "b" is the number inside the second square root.
Multiplication Rule: To multiply \$ \sqrt a \$ and \$ \sqrt b\$, you multiply the numbers inside the radicals.
The result is \$ \sqrt ab \$.
So, \$ \sqrt a \times \sqrt b = \sqrt ab \$.