Lesson Example Discussion Quiz: Class Homework |
Step-1 |
Title: Mean and variance of discrete random variable |
Grade: 9-a Lesson: S4-L2 |
Explanation: Hello Students, time to practice and review the steps for the problem. |
| Step | Type | Explanation | Answer |
|---|---|---|---|
1 |
Problem |
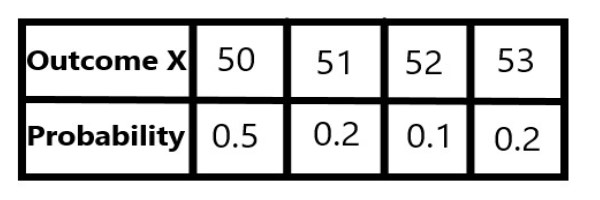
Determine the mean and variance of the random variable X having the following probability distribution. |
|
2 |
Formula: |
Mean E(X) = \$\sum_{i=1}^n x_i p_i(x)\$ |
|
3 |
Step |
Finding the mean |
E(X) = (50×0.5) + (51×0.2) + (52×0.1) + (53×0.2) |
4 |
Step |
Mean |
E(X) = 51 |
5 |
Formula: |
Variance \$VAR(X) = E(X^2) - (E(X))^2\$ |
|
6 |
Step |
Calculating \$E(X^2)\$ |
\$((50^2)×0.5) + ((51^2)×0.2) + ((52^2)×0.1) + ((53^2)×0.2)\$ |
7 |
Step |
After simplification |
\$E(X^2)\$ = 2602.4 |
8 |
Step |
Substitute \$E(X^2)\$ = 2602.4,E(X) = 51 in VAR(X) |
|
9 |
Step |
VAR(X) |
\$2602.4 - 51^2\$ |
10 |
Step |
Simplification |
\$2602.4 - 2601\$ |
11 |
Step |
After simplification |
VAR(X) = 3.1 |
12 |
Step |
Mean and variance |
E(X) = 51, VAR(X) = 3.1 |
13 |
Answer |
B |
|
Tutor: Questions
| Seq | Type | Question | Audio |
|---|---|---|---|
1 |
Problem |
What did you learn from this problem? |
|
2 |
Clue |
What did you learn from the clues? |
|
3 |
Hint |
What did you learn from the Hints? |
|
4 |
Step |
What did you learn from the Steps? |
|
5 |
Step |
How can we improve the Steps? |
Copyright © 2020-2022 saibook.us Contact: info@saibook.us Version: 1.5 Built: 27-February-2023 06:00 AM EST