Lesson Example Discussion Quiz: Class Homework |
Step-5 |
Title: Trigonometry ratios in right triangles |
Grade: 1400-a Lesson: S3-L2 |
Explanation: Hello Students, time to practice and review the steps for the problem. |
Lesson Steps
| Step | Type | Explanation | Answer |
|---|---|---|---|
1 |
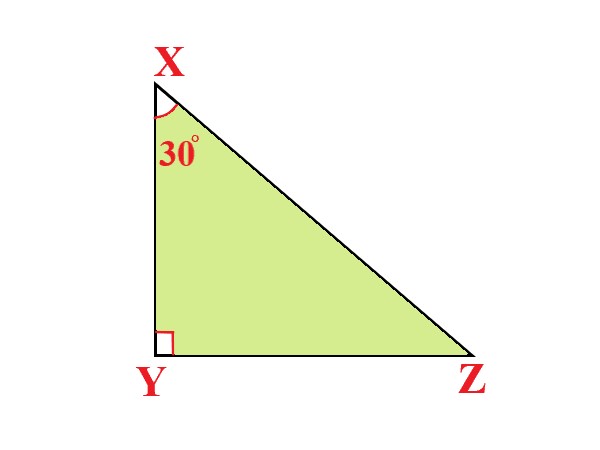
Problem |
In a triangle XYZ, right-angled at Y, XY = 15 inches, and angle \$ X = 30^o\$. Find cos X. |
|
2 |
Step |
The given values are |
XY = 15 inches, \$ X = 30^o\$ |
3 |
Step |
To find the cosine of angle X in the right triangle XYZ, you can use the definition of cosine, which is the ratio of the adjacent side to the hypotenuse. |
|
4 |
Step |
Find the length of side XZ (the hypotenuse) using trigonometric ratios in a right triangle. Using the sine function, we have: |
\$ "cos"("X") = ("Adjacent") / ("Hypotenuse") \$ \$sin(30^o) = "XY"/"XZ"\$ \$1/2 = 15 / "XZ"\$ |
5 |
Step |
Cross multiply: |
\$XZ = 15/(1/2)\$ |
6 |
Step |
Now, calculate cosine X: |
\$cos(X) = "XY" / "XZ"\$ |
7 |
Step |
So, the cosine of angle X is \$1/2\$. |
|
8 |
Choice.A |
Correct representation using the cosine formula |
\$1/2\$ |
9 |
Choice.B |
The cosine function only outputs values between -1 and 1. Therefore, -2 is not a possible value for the cosine function so wrong |
-2 |
10 |
Choice.C |
This is incorrect. It states \$−1/2\$, which is the cosine of 60 degrees, not 30 degrees |
\$-1/2\$ |
11 |
Choice.D |
The cosine of an angle cannot be greater than 1 or less than -1 because the cosine function’s range is between -1 and 1 so wrong |
2 |
12 |
Answer |
Option |
A |
13 |
Sumup |
Can you briefly tell me what you’ve learned and understood in today’s lesson? |
|
Copyright © 2020-2022 saibook.us Contact: info@saibook.us Version: 1.5 Built: 15-May-2024 09:20AM EST