Lesson Example Discussion Quiz: Class Homework |
Step-4 |
Title: Trigonometry ratios in right triangles |
Grade: 1400-a Lesson: S3-L2 |
Explanation: Hello Students, time to practice and review the steps for the problem. |
Lesson Steps
| Step | Type | Explanation | Answer |
|---|---|---|---|
1 |
Problem |
In a right triangle ABC, right-angled at B, If tan A = 1 then find the value 2sinAcosA. |
|
2 |
Step |
The given value is |
tan A = 1 |
3 |
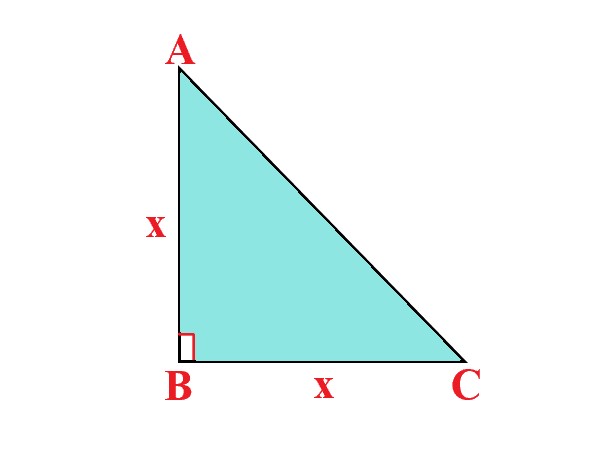
Hint |
If tan A = 1, it means that the length of the side opposite angle A is equal to the length of the adjacent side. Let’s denote this common length as x. |
|
4 |
Formula: |
Since it’s a right-angled triangle, the hypotenuse can be found using the Pythagorean theorem: |
\$"Hypotenuse" = ("Opposite side")^2 + ("Adjacent side")^2\$ |
5 |
Step |
In this case, it becomes: |
\$"Hypotenuse"^2 = "x"^2 + "x"^2\$ \$"Hypotenuse" = (2"x")^2\$ \$"Hypotenuse" = "x"\sqrt(2)\$ |
6 |
Step |
Now, substitute these values into 2sinAcosA |
\$2"sinAcosA"= 2 times ("x" /("x" \sqrt(2))) times ("x" /("x"\sqrt(2)))\$ |
7 |
Step |
Simplify this expression |
\$2"sinAcosA" = 2(1/\sqrt2 times 1/\sqrt2)\$ \$2"sinA cosA" = 2/2\$ |
8 |
Step |
Make it simpler |
2sinA cosA = 1 |
9 |
Step |
So, in this case, when tanA=1, the value of 2sinAcosA is 1. |
|
10 |
Sumup |
Can you summarize what you’ve understood in the above steps? |
|
11 |
Choice.A |
This option is incorrect because it suggests a value of 2, which doesn’t match the correct calculation of 1 |
2 |
12 |
Choice.B |
This is the correct option as it correctly identifies the value of 2sin(A)cos(A) as 1 based on the given condition that tan(A) = 1 |
1 |
13 |
Choice.C |
This option is incorrect because it suggests a value of -1, which doesn’t match the correct calculation of 1 |
-1 |
14 |
Choice.D |
This option is incorrect because it suggests a value of -2, which doesn’t match the correct calculation of 1 |
-2 |
15 |
Answer |
Option |
B |
16 |
Sumup |
Can you summarize what you’ve understood in the above steps? |
|
Copyright © 2020-2022 saibook.us Contact: info@saibook.us Version: 1.5 Built: 15-May-2024 09:20AM EST