Lesson Example Discussion Quiz: Class Homework |
Step-1 |
Title: Trigonometry ratios in right triangles |
Grade: 1400-a Lesson: S3-L2 |
Explanation: Hello Students, time to practice and review the steps for the problem. |
Lesson Steps
| Step | Type | Explanation | Answer |
|---|---|---|---|
1 |
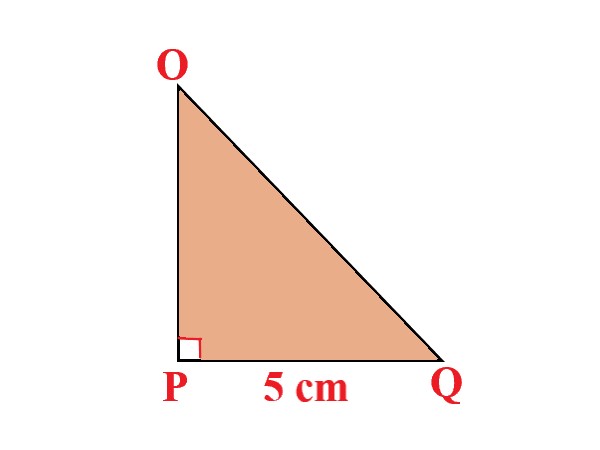
Problem |
In the ∆OPQ, right-angled at P, PQ = 5cm, and OQ - OP = 3cm. Determine the value of sin Q + cos Q. |
|
2 |
Step |
In a right-angled triangle ∆OPQ, we can use the Pythagorean theorem and trigonometric ratios to find sin Q + cos Q. |
|
3 |
Step |
The given values are |
PQ = 5cm, OQ - OP = 3cm |
4 |
Hint |
First, let’s find the length of the sides OQ and OP using the Pythagorean theorem: |
\$ "OQ"^2 = "OP"^2 + "PQ"^2 \$ \$ "OQ"^2 = "OP"^2 + 5^2 \$ |
5 |
Step |
Now, since OQ − OP = 3, we can express OQ in terms of OP: |
OQ = OP + 3 |
6 |
Step |
Now, substitute this into the Pythagorean theorem: |
\$ ("OP" + 3)^2 = "OP"^2 + 5^2 \$ |
7 |
Step |
Expand and simplify the equation: |
\$ "OP"^2 + 9 + 6"OP" = "OP"^2 + 25 \$ |
8 |
Step |
After simplification |
\$ 6"OP" = 16 \$ |
9 |
Step |
Now that we have the value of OP, we can find OQ: |
\$ "OQ" = "OP" + 3 = 8/3 + 3 = 17/3\$ |
10 |
Step |
Now, let’s find the values of sin Q and cos Q: |
\$ "sin" "Q" = ("PQ")/("OQ") = 5/(17/3) = 15/17 \$ \$ "cos" "Q" = ("OP")/("OQ") = (8/3)/(17/3) = 8/17\$ |
11 |
Step |
Substitute the values: |
\$ "sin Q" + "cos Q" = 15/17 + 8/17 \$ \$ "sin Q" + "cos Q" = 23/17 \$ |
12 |
Step |
Therefore, the correct answer is \$ 23/17 \$. |
|
13 |
Choice.A |
This value is approximately 1.41, which isn’t consistent with the expected range of sine and cosine values (between -1 and 1) |
\$ 24/17\$ |
14 |
Choice.B |
This value is approximately 1.03, which is closer to 1 but still outside the valid range for sine and cosine |
\$ 41/40\$ |
15 |
Choice.C |
This value is greater than 1, which is not possible for the sum of sine and cosine in a right triangle |
\$ 33/17\$ |
16 |
Choice.D |
This value falls within the acceptable range (-1 to 1) for the sum of sine and cosine in a right triangle |
\$ 23/17\$ |
17 |
Answer |
Option |
D |
18 |
Sumup |
Can you summarize what you’ve understood in the above steps? |
|
Copyright © 2020-2022 saibook.us Contact: info@saibook.us Version: 1.5 Built: 15-May-2024 09:20AM EST