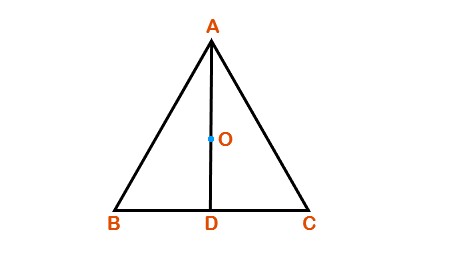
AD is a median of △ABC and O is the centroid such that AO = 10cm. Length of OD is,

Line joining the points (4,5) and (1,2) and passing through the point \$(3,2)\$.
AD is a median of △ABC and O is the centroid and AO = 10 cm.

O is the centroid of the triangle △ABC and is the point of intersection of its three medians.

As the centroid divides a median in the ratio of \$2 : 1\$ from the vertex, in this case we have,

\begin{align} \require{cancel} AO : OD &= 2 : 1 \\ \end{align}

If AO = 10 cm, then OD is

\$\frac{AO}{OD} = \frac{2}{1} \$

Substitute the value.

\$\Rightarrow \frac{10}{OD} = \frac{2}{1} \$

Cancel out common factor.

\$\Rightarrow \frac{ \cancel{10} ^5}{OD} = \frac{ \cancel{2} ^1}{1} \$

Answer

Length of OD is 5 cm.