Lesson Example Discussion Quiz: Class Homework |
Step-5 |
Title: Proving Special Angle Pairs |
Grade: 10-a Lesson: S1-L6 |
Explanation: |
| Step | Type | Explanation | Answer |
|---|---|---|---|
1 |
Problem |
The ray of CD and opposite rays EF and EG. |
|
2 |
Step |
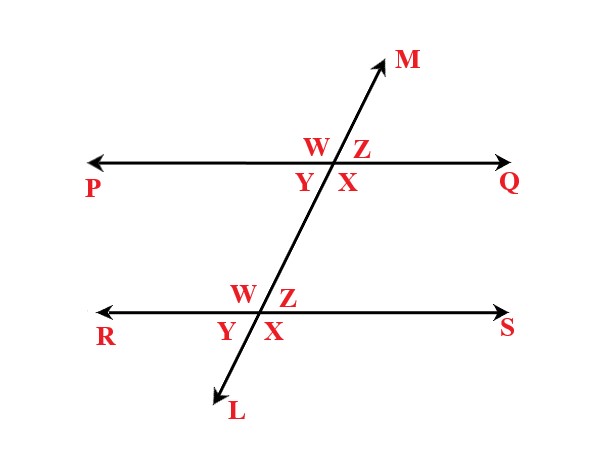
Assume that PQ and RS are the two parallel lines cut by a transversal LM. W, X, Y, Z are the angles created by a transversal At the intersection point on the straight lines PQ and LM |
|
3 |
Step |
PQ is the straight line equation-1 |
\$\angle W + \angle Z = 180°\$ |
4 |
Step |
LM is the straight line equation-2 |
\$\angle X + \angleZ = 180°\$ |
5 |
Step |
So, from (1) and (2), we get |
\$\angle W = \angle x\$ |
6 |
Step |
Again, at the intersection point on the straight lines RS and LM |
|
7 |
Step |
RS is the straight line equation-3 |
stemL[\angle W + \angle Z = 180°] |
8 |
Step |
LM is the straight line equation-4 |
\$\angle W + \angle Y = 180°\$ |
9 |
Step |
So, from (3) and (4), we get |
\$\angle Z = \angle Y\$ |
10 |
Step |
Therefore, it is concluded that the alternate interior angles are congruent. |
|
11 |
Answer |
Hence, the theorem is proved |
|
Copyright © 2020-2022 saibook.us Contact: info@saibook.us Version: 1.5 Built: 30-May-2023 7:45 PM EST