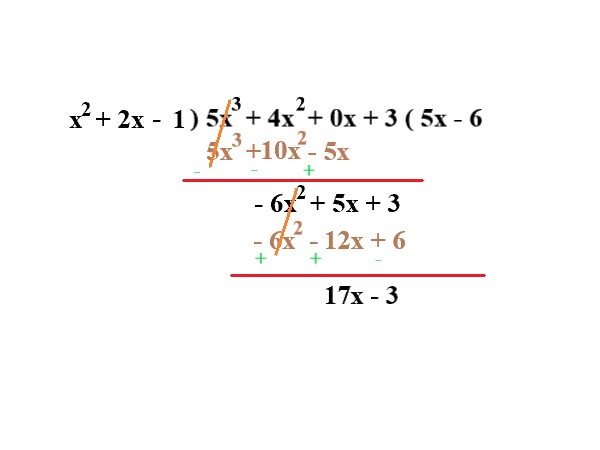Lesson Example Discussion Quiz: Class Homework |
Step-4 |
Title: Dividing polynomials |
Grade: 8-a Lesson: S1-L3 |
Explanation: Hello Students, time to practice and review the steps for the problem. |
Lesson Steps
| Step | Type | Explanation | Answer |
|---|---|---|---|
1 |
Problem |
Divide the following polynomials \$ (5x^3 + 4x^2 + x + 3) ÷ (x^2 + 2x - 1)\$. |
|
2 |
Step |
The given polynomials expression is |
\$ (5x^3 + 4x^2 + x + 3) ÷ (x^2 + 2x -1)\$ |
3 |
Step |
|
|
4 |
Step |
So, the result of the division is \$5x^3 + 4x^2 + x+ 3\$ with a remainder of 17x - 3. |
|
5 |
Step |
Quotient and Remainder: So, the polynomial can be written as |
\$5x - 6 + (17x - 3)/ (x^2 + 2x - 1)\$ |
6 |
Choice.A |
Wrong: The constant term in the remainder should be − 3 instead of + 3 |
\$5x - 6 + (17x + 3) / (x^2 + 2x +1)\$ |
7 |
Choice.B |
Wrong: The constant term in the quotient should be - 6 instead of + 6 |
\$5x + 6 + (17x - 3) / (x^2 + 2x +1)\$ |
8 |
Choice.C |
Option C is correct because it follows the correct form of the division |
\$5x - 6 + (17x - 3) / (x^2 + 2x +1)\$ |
9 |
Choice.D |
The signs in the quotient differ, yielding a remainder of 17x, not -17x as stated wrongly |
\$- 5x + 6 + (-17x - 3) / (x^2 + 2x +1)\$ |
10 |
Answer |
Option |
C |
11 |
Sumup |
Can you summarize what you’ve understood in the above steps? |
|
Copyright © 2020-2022 saibook.us Contact: info@saibook.us Version: 1.5 Built: 19-April-2024 09:20AM EST